You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
NASCAR Pick 'Em 2021 - Texas
- Thread starter pjmolo
- Start date
JJ_14
Go Briscoe!
I'm within striking distance of the top 10. I never thought I'd say that earlier in the season, I was struggling big time.
Team Penske
Team Owner
- Joined
- Jan 16, 2015
- Messages
- 7,759
- Points
- 943
I need some help getting back into the top 25. Are they still paying out to the top 25??
- Joined
- Mar 17, 2014
- Messages
- 39,984
- Points
- 1,033
pjmolo
Director of driver attitude adjustments . . .
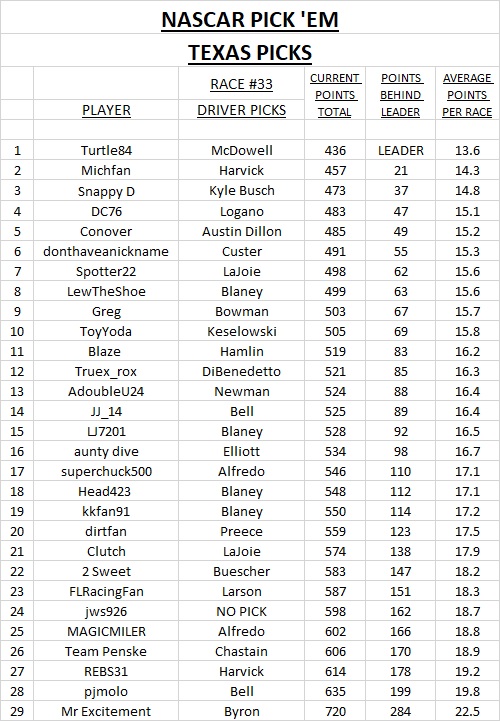
The NASCAR Cup Series begins the third round of its championship playoff format with the running of the Autotrader EchoPark Automotive 500 at Texas Motor Speedway.
The game's most popular driver pick was Ryan Blaney, selected by four players.
Anthony Alfredo, Christopher Bell, Kevin Harvick, and Corey LaJoie were each selected by two.
Good luck to all and thanks for participating.
The game's most popular driver pick was Ryan Blaney, selected by four players.
Anthony Alfredo, Christopher Bell, Kevin Harvick, and Corey LaJoie were each selected by two.
Good luck to all and thanks for participating.

Last edited:
JJ_14
Go Briscoe!
I'll happily take a P3 from Bell! Let's go!
Blaze
The Midnight Rider
Not gonna be on the stage this year. Thanks Dennis
Jorge De Guzman
RESIDENT NASCAR STATESMAN and/or REGIONIONALIST.
- Joined
- Feb 13, 2017
- Messages
- 19,729
- Points
- 883
It’s a 3 horse race now
pjmolo
Director of driver attitude adjustments . . .
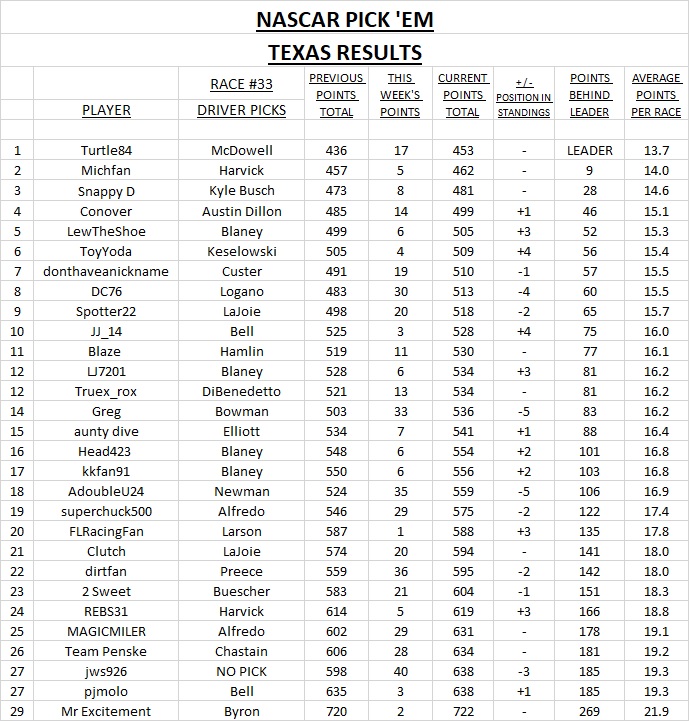
Congrats to @FLRacingFan for taking the "Highest Finishing Pick" award following the first place finish by his pick, Kyle Larson, in the Autotrader EchoPark Automotive 500 at Texas Motor Speedway.
The "Most Upward Movement" award goes to @ToyYoda and @JJ_14 who each moved up four spots in the standings as a result of the finishes by their picks, Brad Keselowski and Christopher Bell.
Congrats to @Turtle84 for holding onto first place in the standings for seven consecutive races.
However, @Michfan has put together a streak of picking a top-ten finisher in each of the last four races and has moved to within nine points of the top of the leader board.
The "Most Upward Movement" award goes to @ToyYoda and @JJ_14 who each moved up four spots in the standings as a result of the finishes by their picks, Brad Keselowski and Christopher Bell.
Congrats to @Turtle84 for holding onto first place in the standings for seven consecutive races.
However, @Michfan has put together a streak of picking a top-ten finisher in each of the last four races and has moved to within nine points of the top of the leader board.
Jorge De Guzman
RESIDENT NASCAR STATESMAN and/or REGIONIONALIST.
- Joined
- Feb 13, 2017
- Messages
- 19,729
- Points
- 883
we got ourselves a Championship Title Fight.
Spotter22
Team Owner
- Joined
- Aug 17, 2017
- Messages
- 14,631
- Points
- 883
My moneys on youwe got ourselves a Championship Title Fight.
Jorge De Guzman
RESIDENT NASCAR STATESMAN and/or REGIONIONALIST.
- Joined
- Feb 13, 2017
- Messages
- 19,729
- Points
- 883
Thanks. I have some good picks left. Hopefully they’re the right ones at the right timeMy moneys on
Spotter22
Team Owner
- Joined
- Aug 17, 2017
- Messages
- 14,631
- Points
- 883
Dont screw it up Snappy!Thanks. I have some good picks left. Hopefully they’re the right ones at the right time
Jorge De Guzman
RESIDENT NASCAR STATESMAN and/or REGIONIONALIST.
- Joined
- Feb 13, 2017
- Messages
- 19,729
- Points
- 883
We’ll try not too. No pressure right?Dont screw it up Snappy!
